| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 7.1) | Exercise 7.1 | Example 6 to 10 (Before Exercise 7.2) |
| Exercise 7.2 | ||
Chapter 7 Coordinate Geometry.
Welcome to the solutions guide for Chapter 7, "Coordinate Geometry," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This chapter significantly enhances the link between algebra and geometry, providing powerful algebraic tools to solve geometric problems involving points, distances, and line segments on the Cartesian plane. Building upon the basics learned in Class 9, this chapter introduces fundamental formulas that allow for precise calculations related to geometric figures defined by coordinates. Mastering these formulas and their applications is essential for various mathematical and scientific disciplines. These comprehensive solutions offer detailed explanations and systematic applications for all exercises within the current syllabus.
A cornerstone of coordinate geometry introduced in this chapter is the Distance Formula. This formula provides a direct method to calculate the straight-line distance between any two points whose coordinates $(x_1, y_1)$ and $(x_2, y_2)$ are known. The solutions meticulously demonstrate the application of the formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$. The applications shown are diverse and fundamental:
- Calculating the length of line segments.
- Determining the lengths of sides and diagonals of polygons (triangles, quadrilaterals) to classify them (e.g., checking if a triangle is isosceles, equilateral, or right-angled using the converse of Pythagoras theorem; checking if a quadrilateral is a parallelogram, rectangle, square, or rhombus).
- Verifying if three or more points are collinear (lie on the same straight line) by checking if the sum of the distances between two pairs of points equals the distance between the remaining pair (e.g., $AB + BC = AC$).
Another fundamental tool introduced is the Section Formula. This formula allows us to find the coordinates of a point that divides the line segment joining two given points $(x_1, y_1)$ and $(x_2, y_2)$ internally in a specified ratio, say $m_1 : m_2$. The solutions demonstrate the precise application of the formula for the coordinates $(x, y)$ of the division point: $x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$ and $y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$. Key applications and special cases covered include:
- Finding the coordinates of a point dividing a segment in a given ratio.
- Deriving and applying the Midpoint Formula, a special case where the ratio is $1:1$, yielding coordinates $(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$. This is frequently used in problems involving medians of triangles or diagonals of parallelograms.
- Finding the ratio in which a given point (or the x-axis or y-axis) divides a line segment joining two points, often by assuming the ratio is $k:1$.
- Solving problems involving points of trisection (dividing a segment into three equal parts, requiring ratios $1:2$ and $2:1$).
Regarding the rationalized syllabus for 2024-25, Chapter 7, "Coordinate Geometry," in the Class 10 NCERT textbook has been significantly streamlined. The section covering the formula for the Area of a Triangle given the coordinates of its vertices, and all related exercises (including applications like checking collinearity using the area formula or finding the area of quadrilaterals), has been completely removed. The curriculum now focuses exclusively on the Distance Formula and the Section Formula and their diverse applications in solving geometric problems. By diligently working through these focused solutions, students can master the application of these two essential formulas, develop proficiency in solving coordinate geometry problems algebraically, and appreciate the power of this analytical approach to geometry.
Example 1 to 5 (Before Exercise 7.1)
Example 1. Do the points (3, 2), (–2, –3) and (2, 3) form a triangle? If so, name the type of triangle formed.
Answer:
Let the given points be A(3, 2), B(–2, –3), and C(2, 3).
To determine if these points form a triangle, we can calculate the distances between each pair of points and check if the sum of the lengths of any two sides is greater than the length of the third side. We will use the distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Calculation of side lengths:
Distance between A(3, 2) and B(–2, –3) (AB):
$AB = \sqrt{(-2-3)^2 + (-3-2)^2}$
$AB = \sqrt{(-5)^2 + (-5)^2}$
$AB = \sqrt{25 + 25}$
$AB = \sqrt{50}$
$AB = 5\sqrt{2}$ units.
Distance between B(–2, –3) and C(2, 3) (BC):
$BC = \sqrt{(2-(-2))^2 + (3-(-3))^2}$
$BC = \sqrt{(2+2)^2 + (3+3)^2}$
$BC = \sqrt{4^2 + 6^2}$
$BC = \sqrt{16 + 36}$
$BC = \sqrt{52}$
$BC = 2\sqrt{13}$ units.
Distance between A(3, 2) and C(2, 3) (AC):
$AC = \sqrt{(2-3)^2 + (3-2)^2}$
$AC = \sqrt{(-1)^2 + (1)^2}$
$AC = \sqrt{1 + 1}$
$AC = \sqrt{2}$ units.
Check if the points form a triangle:
For the points to form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
$AB = 5\sqrt{2} \approx 5 \times 1.414 = 7.07$
$BC = 2\sqrt{13} \approx 2 \times 3.606 = 7.212$
$AC = \sqrt{2} \approx 1.414$
Let's check the triangle inequalities:
$AB + AC = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \approx 8.485$. Is $6\sqrt{2} > \sqrt{52}$? $(6\sqrt{2})^2 = 36 \times 2 = 72$, $(\sqrt{52})^2 = 52$. Since $72 > 52$, $6\sqrt{2} > \sqrt{52}$. Thus, $AB + AC > BC$.
$AB + BC = \sqrt{50} + \sqrt{52} \approx 7.07 + 7.212 = 14.282$. Is $14.282 > \sqrt{2} \approx 1.414$? Yes.
$BC + AC = \sqrt{52} + \sqrt{2} \approx 7.212 + 1.414 = 8.626$. Is $8.626 > \sqrt{50} \approx 7.07$? Yes.
Since the sum of the lengths of any two sides is greater than the length of the third side, the points A, B, and C form a triangle.
Determine the type of triangle:
The lengths of the sides are $\sqrt{50}$, $\sqrt{52}$, and $\sqrt{2}$. Since all three side lengths are different, the triangle is a scalene triangle.
Let's check if it is a right-angled triangle using the Pythagorean theorem ($a^2 + b^2 = c^2$). We check if the square of the longest side is equal to the sum of the squares of the other two sides.
The squares of the sides are: $(\sqrt{50})^2 = 50$, $(\sqrt{52})^2 = 52$, $(\sqrt{2})^2 = 2$.
The longest side is BC with length $\sqrt{52}$. Let's check if $AB^2 + AC^2 = BC^2$:
$(\sqrt{50})^2 + (\sqrt{2})^2 = 50 + 2 = 52$
$(\sqrt{52})^2 = 52$
Since $AB^2 + AC^2 = BC^2$, the Pythagorean theorem holds true. This means that the angle opposite to side BC, which is $\angle$BAC (angle at vertex A), is a right angle ($90^\circ$).
Therefore, the triangle is also a right-angled triangle.
Conclusion:
Based on the side lengths and angle properties, the triangle formed is a scalene right-angled triangle.
Example 2. Show that the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a square
Answer:
Let the given points be A(1, 7), B(4, 2), C(–1, –1), and D(–4, 4) in order.
To show that these points are the vertices of a square, we need to prove that all four sides are equal in length and that the two diagonals are equal in length.
We will use the distance formula between two points $(x_1, y_1)$ and $(x_2, y_2)$, which is $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Calculation of Side Lengths:
Distance between A(1, 7) and B(4, 2) (AB):
$AB = \sqrt{(4-1)^2 + (2-7)^2}$
$AB = \sqrt{(3)^2 + (-5)^2}$
$AB = \sqrt{9 + 25}$
$AB = \sqrt{34}$ units.
Distance between B(4, 2) and C(–1, –1) (BC):
$BC = \sqrt{(-1-4)^2 + (-1-2)^2}$
$BC = \sqrt{(-5)^2 + (-3)^2}$
$BC = \sqrt{25 + 9}$
$BC = \sqrt{34}$ units.
Distance between C(–1, –1) and D(–4, 4) (CD):
$CD = \sqrt{(-4-(-1))^2 + (4-(-1))^2}$
$CD = \sqrt{(-4+1)^2 + (4+1)^2}$
$CD = \sqrt{(-3)^2 + (5)^2}$
$CD = \sqrt{9 + 25}$
$CD = \sqrt{34}$ units.
Distance between D(–4, 4) and A(1, 7) (DA):
$DA = \sqrt{(1-(-4))^2 + (7-4)^2}$
$DA = \sqrt{(1+4)^2 + (3)^2}$
$DA = \sqrt{(5)^2 + 9}$
$DA = \sqrt{25 + 9}$
$DA = \sqrt{34}$ units.
Since $AB = BC = CD = DA = \sqrt{34}$, all four sides are equal in length.
Calculation of Diagonal Lengths:
Distance between A(1, 7) and C(–1, –1) (AC):
$AC = \sqrt{(-1-1)^2 + (-1-7)^2}$
$AC = \sqrt{(-2)^2 + (-8)^2}$
$AC = \sqrt{4 + 64}$
$AC = \sqrt{68}$ units.
Distance between B(4, 2) and D(–4, 4) (BD):
$BD = \sqrt{(-4-4)^2 + (4-2)^2}$
$BD = \sqrt{(-8)^2 + (2)^2}$
$BD = \sqrt{64 + 4}$
$BD = \sqrt{68}$ units.
Since $AC = BD = \sqrt{68}$, the two diagonals are equal in length.
Conclusion:
Since all four sides are equal in length ($AB = BC = CD = DA$) and the two diagonals are equal in length ($AC = BD$), the given points (1, 7), (4, 2), (–1, –1), and (– 4, 4) are the vertices of a square.
Example 3. Fig. 7.6 shows the arrangement of desks in a classroom. Ashima, Bharti and Camella are seated at A(3, 1), B(6, 4) and C(8, 6) respectively. Do you think they are seated in a line? Give reasons for your answer.

Answer:
Let the positions of Ashima, Bharti, and Camella be represented by the points A(3, 1), B(6, 4), and C(8, 6), respectively.
To determine if these points are seated in a line (i.e., are collinear), we can calculate the distances between each pair of points and check if the sum of the lengths of any two segments equals the length of the third segment.
We use the distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Calculation of Distances:
Distance between A(3, 1) and B(6, 4) (AB):
$AB = \sqrt{(6-3)^2 + (4-1)^2}$
$AB = \sqrt{(3)^2 + (3)^2}$
$AB = \sqrt{9 + 9}$
$AB = \sqrt{18}$
$AB = 3\sqrt{2}$ units.
Distance between B(6, 4) and C(8, 6) (BC):
$BC = \sqrt{(8-6)^2 + (6-4)^2}$
$BC = \sqrt{(2)^2 + (2)^2}$
$BC = \sqrt{4 + 4}$
$BC = \sqrt{8}$
$BC = 2\sqrt{2}$ units.
Distance between A(3, 1) and C(8, 6) (AC):
$AC = \sqrt{(8-3)^2 + (6-1)^2}$
$AC = \sqrt{(5)^2 + (5)^2}$
$AC = \sqrt{25 + 25}$
$AC = \sqrt{50}$
$AC = 5\sqrt{2}$ units.
Check for Collinearity:
The points A, B, and C are collinear if the sum of the lengths of the two shorter segments is equal to the length of the longest segment.
The lengths are $AB = 3\sqrt{2}$, $BC = 2\sqrt{2}$, and $AC = 5\sqrt{2}$.
The two shorter lengths are AB and BC. The longest length is AC.
Let's check if $AB + BC = AC$:
$3\sqrt{2} + 2\sqrt{2} = (3+2)\sqrt{2} = 5\sqrt{2}$.
We have $AB + BC = 5\sqrt{2}$ and $AC = 5\sqrt{2}$.
Since $AB + BC = AC$, the points A, B, and C are collinear.
Reason:
The points A, B, and C are collinear because the sum of the distances between two pairs of points (AB and BC) is equal to the distance between the remaining pair of points (AC). When three points are collinear, they lie on the same straight line, and thus the distance between the two extreme points is the sum of the distances between the middle point and each of the extreme points.
Conclusion:
Yes, Ashima, Bharti, and Camella are seated in a line because the points representing their positions are collinear.
Example 4. Find a relation between x and y such that the point (x , y) is equidistant from the points (7, 1) and (3, 5).
Answer:
Given:
A point P(x, y) which is equidistant from point A(7, 1) and point B(3, 5).
To Find:
A relation between x and y.
Solution:
Let the point be P(x, y). The two given points are A(7, 1) and B(3, 5).
According to the problem, the distance of P from A is equal to the distance of P from B.
$PA = PB$
We use the distance formula, which states that the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Using the distance formula for PA and PB:
$PA = \sqrt{(x-7)^2 + (y-1)^2}$
$PB = \sqrt{(x-3)^2 + (y-5)^2}$
Since $PA = PB$, we have:
$\sqrt{(x-7)^2 + (y-1)^2} = \sqrt{(x-3)^2 + (y-5)^2}$
Squaring both sides to eliminate the square root:
$(x-7)^2 + (y-1)^2 = (x-3)^2 + (y-5)^2$
Expand the squared terms using the identity $(a-b)^2 = a^2 - 2ab + b^2$:
$(x^2 - 2(x)(7) + 7^2) + (y^2 - 2(y)(1) + 1^2) = (x^2 - 2(x)(3) + 3^2) + (y^2 - 2(y)(5) + 5^2)$
$(x^2 - 14x + 49) + (y^2 - 2y + 1) = (x^2 - 6x + 9) + (y^2 - 10y + 25)$
Combine the constant terms on each side:
$x^2 - 14x + y^2 - 2y + 50 = x^2 - 6x + y^2 - 10y + 34$
Subtract $x^2$ and $y^2$ from both sides of the equation:
$-14x - 2y + 50 = -6x - 10y + 34$
Move all terms to one side to form the relation. Let's move terms from the right side to the left side:
$-14x + 6x - 2y + 10y + 50 - 34 = 0$
Combine the like terms:
$(-14x + 6x) + (-2y + 10y) + (50 - 34) = 0$
$-8x + 8y + 16 = 0$
To simplify, divide the entire equation by -8:
$\frac{-8x}{-8} + \frac{8y}{-8} + \frac{16}{-8} = \frac{0}{-8}$
$x - y - 2 = 0$
This is the required relation between x and y.
The relation can also be expressed as $x - y = 2$ or $y = x - 2$. This equation represents the perpendicular bisector of the line segment joining points A and B.
Example 5. Find a point on the y-axis which is equidistant from the points A(6,5) and B(– 4, 3).
Answer:
Given:
Two points A(6, 5) and B(-4, 3).
A point P lies on the y-axis and is equidistant from A and B.
To Find:
The coordinates of the point P on the y-axis.
Solution:
Let the point on the y-axis be P. Since the point lies on the y-axis, its x-coordinate must be 0. So, the coordinates of P are (0, y).
The given points are A(6, 5) and B(-4, 3).
According to the problem, point P is equidistant from points A and B. This means the distance PA is equal to the distance PB.
$PA = PB$
We can use the distance formula between two points $(x_1, y_1)$ and $(x_2, y_2)$, which is $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Distance PA is the distance between P(0, y) and A(6, 5):
$PA = \sqrt{(6-0)^2 + (5-y)^2} = \sqrt{6^2 + (5-y)^2} = \sqrt{36 + (5-y)^2}$
Distance PB is the distance between P(0, y) and B(-4, 3):
$PB = \sqrt{(-4-0)^2 + (3-y)^2} = \sqrt{(-4)^2 + (3-y)^2} = \sqrt{16 + (3-y)^2}$
Since $PA = PB$, we can equate their squares to simplify the calculation and remove the square root:
$PA^2 = PB^2$
$(36 + (5-y)^2) = (16 + (3-y)^2)$
Expand the squared terms using the identity $(a-b)^2 = a^2 - 2ab + b^2$:
$36 + (5^2 - 2(5)(y) + y^2) = 16 + (3^2 - 2(3)(y) + y^2)$
$36 + (25 - 10y + y^2) = 16 + (9 - 6y + y^2)$
$36 + 25 - 10y + y^2 = 16 + 9 - 6y + y^2$
Combine the constant terms on each side:
$61 - 10y + y^2 = 25 - 6y + y^2$
Subtract $y^2$ from both sides of the equation:
$61 - 10y = 25 - 6y$
Now, we need to solve for y. Let's move the terms involving y to one side and the constant terms to the other side.
Add $10y$ to both sides:
$61 = 25 - 6y + 10y$
$61 = 25 + 4y$
Subtract 25 from both sides:
$61 - 25 = 4y$
$36 = 4y$
Divide both sides by 4:
$\frac{36}{4} = y$
$9 = y$
So, the value of y is 9.
The coordinates of the point P on the y-axis are (0, y).
Therefore, the point is (0, 9).
The point on the y-axis equidistant from A(6,5) and B(–4, 3) is (0, 9).
Exercise 7.1
Question 1. Find the distance between the following pairs of points :
(i) (2, 3), (4, 1)
(ii) (– 5, 7), (– 1, 3)
(iii) (a, b), (– a, – b)
Answer:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
(i) Points (2, 3) and (4, 1)
Let $(x_1, y_1) = (2, 3)$ and $(x_2, y_2) = (4, 1)$.
Using the distance formula:
$d = \sqrt{(4-2)^2 + (1-3)^2}$
$d = \sqrt{(2)^2 + (-2)^2}$
$d = \sqrt{4 + 4}$
$d = \sqrt{8}$
We can simplify $\sqrt{8}$ as $\sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}$.
The distance between (2, 3) and (4, 1) is $2\sqrt{2}$ units.
(ii) Points (– 5, 7) and (– 1, 3)
Let $(x_1, y_1) = (-5, 7)$ and $(x_2, y_2) = (-1, 3)$.
Using the distance formula:
$d = \sqrt{(-1 - (-5))^2 + (3-7)^2}$
$d = \sqrt{(-1 + 5)^2 + (-4)^2}$
$d = \sqrt{(4)^2 + (-4)^2}$
$d = \sqrt{16 + 16}$
$d = \sqrt{32}$
We can simplify $\sqrt{32}$ as $\sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4\sqrt{2}$.
The distance between (– 5, 7) and (– 1, 3) is $4\sqrt{2}$ units.
(iii) Points (a, b) and (– a, – b)
Let $(x_1, y_1) = (a, b)$ and $(x_2, y_2) = (-a, -b)$.
Using the distance formula:
$d = \sqrt{(-a - a)^2 + (-b - b)^2}$
$d = \sqrt{(-2a)^2 + (-2b)^2}$
$d = \sqrt{4a^2 + 4b^2}$
$d = \sqrt{4(a^2 + b^2)}$
$d = \sqrt{4} \sqrt{a^2 + b^2}$
$d = 2\sqrt{a^2 + b^2}$
The distance between (a, b) and (– a, – b) is $2\sqrt{a^2 + b^2}$ units.
Question 2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
Towns provided in Section 7.2 - A town B is located 36 km east and 15 km north of the town A. How would you find the distance from town A to town B without actually measuring it.
Answer:
Given:
Points: (0, 0) and (36, 15).
Town B is 36 km east and 15 km north of Town A.
To Find:
The distance between the points (0, 0) and (36, 15).
The distance between Town A and Town B.
Solution:
To find the distance between two points, we use the distance formula in coordinate geometry.
The distance $ d $ between two points $ (x_1, y_1) $ and $ (x_2, y_2) $ is given by:
$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $
Let's find the distance between the points (0, 0) and (36, 15).
Here, $ (x_1, y_1) = (0, 0) $ and $ (x_2, y_2) = (36, 15) $.
Substitute these values into the distance formula:
$ d = \sqrt{(36 - 0)^2 + (15 - 0)^2} $
$ d = \sqrt{(36)^2 + (15)^2} $
Now, calculate the squares:
$ 36^2 = 36 \times 36 = 1296 $
$ 15^2 = 15 \times 15 = 225 $
Substitute these values back into the formula:
$ d = \sqrt{1296 + 225} $
$ d = \sqrt{1521} $
To find the square root of 1521, we can check perfect squares or use prime factorisation. Let's use a known square or estimate. $ 30^2 = 900 $ and $ 40^2 = 1600 $. Since the number ends in 1, its square root must end in 1 or 9. Let's try 39.
$ 39^2 = 39 \times 39 = 1521 $
So,
$ d = 39 $
The distance between the points (0, 0) and (36, 15) is 39 units.
Now, let's consider the problem of finding the distance between Town A and Town B.
Town B is located 36 km east and 15 km north of Town A.
We can model this situation using a coordinate system. Let Town A be placed at the origin (0, 0) of the coordinate plane. The east direction can be taken along the positive x-axis, and the north direction along the positive y-axis.
Since Town B is 36 km east of Town A, its x-coordinate will be 36.
Since Town B is 15 km north of Town A, its y-coordinate will be 15.
So, the coordinates of Town A are $ (0, 0) $ and the coordinates of Town B are $ (36, 15) $.
The distance between Town A and Town B is the distance between the points $ (0, 0) $ and $ (36, 15) $ in this coordinate system. This is exactly the same problem we solved above.
Using the distance formula again for $ (0, 0) $ and $ (36, 15) $:
$ d = \sqrt{(36 - 0)^2 + (15 - 0)^2} $
$ d = \sqrt{36^2 + 15^2} $
$ d = \sqrt{1296 + 225} $
$ d = \sqrt{1521} $
$ d = 39 $
The distance between the two towns A and B is 39 km.
We can find this distance without actually measuring it by representing the locations of the towns as points on a coordinate plane and applying the distance formula.
Answer:
The distance between the points (0, 0) and (36, 15) is 39 units.
Yes, we can find the distance between the two towns A and B. By representing Town A at (0, 0) and Town B at (36, 15) on a coordinate plane, the distance between them is found using the distance formula to be 39 km.
Question 3. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.
Answer:
Given:
Three points: A(1, 5), B(2, 3), and C(-2, -11).
To Determine:
If the given points are collinear.
Solution:
Points are collinear if the sum of the lengths of any two line segments formed by the points is equal to the length of the third line segment.
Let's find the distances between each pair of points using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Distance between A(1, 5) and B(2, 3) (AB):
$AB = \sqrt{(2-1)^2 + (3-5)^2}$
$AB = \sqrt{(1)^2 + (-2)^2}$
$AB = \sqrt{1 + 4}$
$AB = \sqrt{5}$
Distance between B(2, 3) and C(-2, -11) (BC):
$BC = \sqrt{(-2-2)^2 + (-11-3)^2}$
$BC = \sqrt{(-4)^2 + (-14)^2}$
$BC = \sqrt{16 + 196}$
$BC = \sqrt{212}$
We can simplify $\sqrt{212}$ as $\sqrt{4 \times 53} = \sqrt{4} \times \sqrt{53} = 2\sqrt{53}$.
$BC = 2\sqrt{53}$
Distance between A(1, 5) and C(-2, -11) (AC):
$AC = \sqrt{(-2-1)^2 + (-11-5)^2}$
$AC = \sqrt{(-3)^2 + (-16)^2}$
$AC = \sqrt{9 + 256}$
$AC = \sqrt{265}$
Now, let's check if the sum of any two distances is equal to the third distance.
$AB = \sqrt{5} \approx 2.236$
$BC = \sqrt{212} \approx 14.560$
$AC = \sqrt{265} \approx 16.279$
Check if $AB + BC = AC$:
$\sqrt{5} + \sqrt{212} = \sqrt{265}$
$2.236 + 14.560 = 16.796$
$16.796 \neq 16.279$
Check if $AB + AC = BC$:
$\sqrt{5} + \sqrt{265} = \sqrt{212}$
$2.236 + 16.279 = 18.515$
$18.515 \neq 14.560$
Check if $BC + AC = AB$:
$\sqrt{212} + \sqrt{265} = \sqrt{5}$
$14.560 + 16.279 = 30.839$
$30.839 \neq 2.236$
Since the sum of the lengths of any two segments is not equal to the length of the third segment, the points are not collinear.
Therefore, the points (1, 5), (2, 3), and (– 2, – 11) are not collinear.
Question 4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Answer:
Given:
Three points: A(5, -2), B(6, 4), and C(7, -2).
To Check:
Whether the given points are the vertices of an isosceles triangle.
Solution:
An isosceles triangle is a triangle that has at least two sides of equal length.
We will calculate the distance between each pair of points using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Let the points be A(5, -2), B(6, 4), and C(7, -2).
Distance between A(5, -2) and B(6, 4) (Length of AB):
$AB = \sqrt{(6-5)^2 + (4-(-2))^2}$
$AB = \sqrt{(1)^2 + (4+2)^2}$
$AB = \sqrt{1^2 + 6^2}$
$AB = \sqrt{1 + 36}$
$AB = \sqrt{37}$
Distance between B(6, 4) and C(7, -2) (Length of BC):
$BC = \sqrt{(7-6)^2 + (-2-4)^2}$
$BC = \sqrt{(1)^2 + (-6)^2}$
$BC = \sqrt{1 + 36}$
$BC = \sqrt{37}$
Distance between A(5, -2) and C(7, -2) (Length of AC):
$AC = \sqrt{(7-5)^2 + (-2-(-2))^2}$
$AC = \sqrt{(2)^2 + (-2+2)^2}$
$AC = \sqrt{2^2 + 0^2}$
$AC = \sqrt{4 + 0}$
$AC = \sqrt{4}$
$AC = 2$
Comparing the lengths of the sides:
$AB = \sqrt{37}$
$BC = \sqrt{37}$
$AC = 2$
Since the lengths of two sides, AB and BC, are equal ($AB = BC = \sqrt{37}$), the triangle ABC is an isosceles triangle.
Therefore, the points (5, – 2), (6, 4), and (7, – 2) are the vertices of an isosceles triangle.
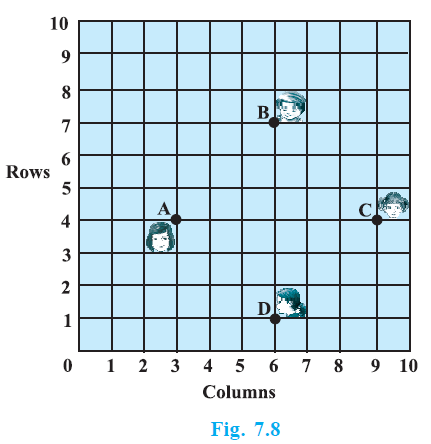
Question 5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
Answer:
Given:
The positions of 4 friends A, B, C, and D in a classroom, represented by points on a coordinate grid in Fig. 7.8.
To Determine:
Whether the points A, B, C, and D form a square using the distance formula and determine who is correct between Champa and Chameli.
Solution:
From the given figure (Fig. 7.8), we can determine the coordinates of the points A, B, C, and D.
Point A is at (3, 4).
Point B is at (6, 7).
Point C is at (9, 4).
Point D is at (6, 1).
For a quadrilateral to be a square, all four sides must be equal in length, and the two diagonals must also be equal in length.
We will calculate the distance between each pair of adjacent vertices (sides) and the distance between opposite vertices (diagonals) using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Calculating the lengths of the sides:
Length of AB (distance between A(3, 4) and B(6, 7)):
$AB = \sqrt{(6-3)^2 + (7-4)^2} = \sqrt{(3)^2 + (3)^2} = \sqrt{9 + 9} = \sqrt{18}$
$AB = \sqrt{9 \times 2} = 3\sqrt{2}$ units.
Length of BC (distance between B(6, 7) and C(9, 4)):
$BC = \sqrt{(9-6)^2 + (4-7)^2} = \sqrt{(3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18}$
$BC = \sqrt{9 \times 2} = 3\sqrt{2}$ units.
Length of CD (distance between C(9, 4) and D(6, 1)):
$CD = \sqrt{(6-9)^2 + (1-4)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18}$
$CD = \sqrt{9 \times 2} = 3\sqrt{2}$ units.
Length of DA (distance between D(6, 1) and A(3, 4)):
$DA = \sqrt{(3-6)^2 + (4-1)^2} = \sqrt{(-3)^2 + (3)^2} = \sqrt{9 + 9} = \sqrt{18}$
$DA = \sqrt{9 \times 2} = 3\sqrt{2}$ units.
From the side length calculations, we see that $AB = BC = CD = DA = 3\sqrt{2}$. All four sides are equal.
Calculating the lengths of the diagonals:
Length of AC (distance between A(3, 4) and C(9, 4)):
$AC = \sqrt{(9-3)^2 + (4-4)^2} = \sqrt{(6)^2 + (0)^2} = \sqrt{36 + 0} = \sqrt{36}$
$AC = 6$ units.
Length of BD (distance between B(6, 7) and D(6, 1)):
$BD = \sqrt{(6-6)^2 + (1-7)^2} = \sqrt{(0)^2 + (-6)^2} = \sqrt{0 + 36} = \sqrt{36}$
$BD = 6$ units.
From the diagonal length calculations, we see that $AC = BD = 6$. The two diagonals are equal.
Since all four sides of the quadrilateral ABCD are equal ($AB = BC = CD = DA$) and the two diagonals are also equal ($AC = BD$), the quadrilateral ABCD is a square.
Therefore, Champa's statement that ABCD is a square is correct.
Champa is correct.
Question 6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
To determine the type of quadrilateral, we will calculate the lengths of all four sides and the two diagonals using the distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
(i) Points A(– 1, – 2), B(1, 0), C(– 1, 2), D(– 3, 0)
Length of AB:
$AB = \sqrt{(1 - (-1))^2 + (0 - (-2))^2} = \sqrt{(1+1)^2 + (0+2)^2} = \sqrt{2^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
Length of BC:
$BC = \sqrt{(-1 - 1)^2 + (2 - 0)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
Length of CD:
$CD = \sqrt{(-3 - (-1))^2 + (0 - 2)^2} = \sqrt{(-3+1)^2 + (-2)^2} = \sqrt{(-2)^2 + (-2)^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
Length of DA:
$DA = \sqrt{(-1 - (-3))^2 + (-2 - 0)^2} = \sqrt{(-1+3)^2 + (-2)^2} = \sqrt{2^2 + (-2)^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
All four sides are equal in length: $AB = BC = CD = DA = 2\sqrt{2}$.
Now, let's calculate the lengths of the diagonals AC and BD.
Length of AC:
$AC = \sqrt{(-1 - (-1))^2 + (2 - (-2))^2} = \sqrt{(-1+1)^2 + (2+2)^2} = \sqrt{0^2 + 4^2} = \sqrt{0 + 16} = \sqrt{16} = 4$
Length of BD:
$BD = \sqrt{(-3 - 1)^2 + (0 - 0)^2} = \sqrt{(-4)^2 + 0^2} = \sqrt{16 + 0} = \sqrt{16} = 4$
The diagonals are equal in length: $AC = BD = 4$.
Since all sides are equal and the diagonals are equal, the quadrilateral formed by the points is a Square.
(ii) Points A(–3, 5), B(3, 1), C(0, 3), D(–1, – 4)
Length of AB:
$AB = \sqrt{(3 - (-3))^2 + (1 - 5)^2} = \sqrt{(3+3)^2 + (-4)^2} = \sqrt{6^2 + 16} = \sqrt{36 + 16} = \sqrt{52}$
Length of BC:
$BC = \sqrt{(0 - 3)^2 + (3 - 1)^2} = \sqrt{(-3)^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13}$
Length of CD:
$CD = \sqrt{(-1 - 0)^2 + (-4 - 3)^2} = \sqrt{(-1)^2 + (-7)^2} = \sqrt{1 + 49} = \sqrt{50}$
Length of DA:
$DA = \sqrt{(-3 - (-1))^2 + (5 - (-4))^2} = \sqrt{(-3+1)^2 + (5+4)^2} = \sqrt{(-2)^2 + 9^2} = \sqrt{4 + 81} = \sqrt{85}$
The side lengths are $AB = \sqrt{52}$, $BC = \sqrt{13}$, $CD = \sqrt{50}$, $DA = \sqrt{85}$. None of the adjacent or opposite sides are equal.
Now, let's calculate the lengths of the diagonals AC and BD.
Length of AC:
$AC = \sqrt{(0 - (-3))^2 + (3 - 5)^2} = \sqrt{(0+3)^2 + (-2)^2} = \sqrt{3^2 + 4} = \sqrt{9 + 4} = \sqrt{13}$
Length of BD:
$BD = \sqrt{(-1 - 3)^2 + (-4 - 1)^2} = \sqrt{(-4)^2 + (-5)^2} = \sqrt{16 + 25} = \sqrt{41}$
The diagonal lengths are $AC = \sqrt{13}$ and $BD = \sqrt{41}$. The diagonals are not equal.
Since no sides are equal and the diagonals are not equal, and one side length is equal to one diagonal length ($BC = AC = \sqrt{13}$), the points do not form a standard quadrilateral like a square, rhombus, rectangle, or parallelogram. These points form a General Quadrilateral.
(iii) Points A(4, 5), B(7, 6), C(4, 3), D(1, 2)
Length of AB:
$AB = \sqrt{(7 - 4)^2 + (6 - 5)^2} = \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10}$
Length of BC:
$BC = \sqrt{(4 - 7)^2 + (3 - 6)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18}$
Length of CD:
$CD = \sqrt{(1 - 4)^2 + (2 - 3)^2} = \sqrt{(-3)^2 + (-1)^2} = \sqrt{9 + 1} = \sqrt{10}$
Length of DA:
$DA = \sqrt{(4 - 1)^2 + (5 - 2)^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18}$
We observe that opposite sides are equal: $AB = CD = \sqrt{10}$ and $BC = DA = \sqrt{18}$. This indicates it could be a parallelogram or a rectangle.
Now, let's calculate the lengths of the diagonals AC and BD.
Length of AC:
$AC = \sqrt{(4 - 4)^2 + (3 - 5)^2} = \sqrt{0^2 + (-2)^2} = \sqrt{0 + 4} = \sqrt{4} = 2$
Length of BD:
$BD = \sqrt{(1 - 7)^2 + (2 - 6)^2} = \sqrt{(-6)^2 + (-4)^2} = \sqrt{36 + 16} = \sqrt{52}$
The diagonal lengths are $AC = 2$ and $BD = \sqrt{52}$. The diagonals are not equal ($2 \neq \sqrt{52}$).
Since opposite sides are equal and the diagonals are not equal, the quadrilateral formed by the points is a Parallelogram.
Question 7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
Answer:
Given:
Two points A(2, -5) and B(-2, 9).
A point P lies on the x-axis and is equidistant from A and B.
To Find:
The coordinates of the point P on the x-axis.
Solution:
Let the point on the x-axis be P. Since the point lies on the x-axis, its y-coordinate must be 0. So, the coordinates of P are (x, 0).
The given points are A(2, -5) and B(-2, 9).
According to the problem, point P is equidistant from points A and B. This means the distance PA is equal to the distance PB.
$PA = PB$
We can use the distance formula between two points $(x_1, y_1)$ and $(x_2, y_2)$, which is $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Distance PA is the distance between P(x, 0) and A(2, -5):
$PA = \sqrt{(2-x)^2 + (-5-0)^2} = \sqrt{(2-x)^2 + (-5)^2} = \sqrt{(2-x)^2 + 25}$
Distance PB is the distance between P(x, 0) and B(-2, 9):
$PB = \sqrt{(-2-x)^2 + (9-0)^2} = \sqrt{(-2-x)^2 + 9^2} = \sqrt{(-2-x)^2 + 81}$
Since $PA = PB$, we can equate their squares to simplify the calculation and remove the square root:
$PA^2 = PB^2$
$(2-x)^2 + 25 = (-2-x)^2 + 81$
Expand the squared terms using the identity $(a-b)^2 = a^2 - 2ab + b^2$ and $(a+b)^2 = a^2 + 2ab + b^2$ (note that $(-2-x)^2 = (-(2+x))^2 = (2+x)^2$):
$(2^2 - 2(2)(x) + x^2) + 25 = ((-2)^2 - 2(-2)(x) + x^2) + 81$
$(4 - 4x + x^2) + 25 = (4 + 4x + x^2) + 81$
Combine the constant terms on each side:
$x^2 - 4x + 29 = x^2 + 4x + 85$
Subtract $x^2$ from both sides of the equation:
$-4x + 29 = 4x + 85$
Move the terms involving x to one side and the constant terms to the other side.
Subtract $4x$ from both sides:
$-4x - 4x + 29 = 85$
$-8x + 29 = 85$
Subtract 29 from both sides:
$-8x = 85 - 29$
$-8x = 56$
Divide both sides by -8:
$x = \frac{56}{-8}$
$x = -7$
So, the value of x is -7.
The coordinates of the point P on the x-axis are (x, 0).
Therefore, the point is (-7, 0).
The point on the x-axis equidistant from (2, –5) and (–2, 9) is (-7, 0).
Question 8. Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Answer:
Given:
Two points P(2, -3) and Q(10, y).
The distance between points P and Q is 10 units.
To Find:
The values of y.
Solution:
Let the points be P$(x_1, y_1) = (2, -3)$ and Q$(x_2, y_2) = (10, y)$.
The distance between P and Q is given as $PQ = 10$ units.
We use the distance formula:
$PQ = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Substitute the given values into the formula:
$10 = \sqrt{(10-2)^2 + (y - (-3))^2}$
Simplify the terms inside the square root:
$10 = \sqrt{(8)^2 + (y+3)^2}$
$10 = \sqrt{64 + (y+3)^2}$
To remove the square root, square both sides of the equation:
$10^2 = (\sqrt{64 + (y+3)^2})^2$
$100 = 64 + (y+3)^2$
Subtract 64 from both sides:
$100 - 64 = (y+3)^2$
$36 = (y+3)^2$
Take the square root of both sides. Remember that the square root of a number has both positive and negative values:
$\sqrt{36} = \pm \sqrt{(y+3)^2}$
$\pm 6 = y+3$
We now have two possible cases for the value of y:
Case 1:
$6 = y+3$
Subtract 3 from both sides:
$y = 6 - 3$
$y = 3$
Case 2:
$-6 = y+3$
Subtract 3 from both sides:
$y = -6 - 3$
$y = -9$
Thus, there are two possible values for y.
The values of y for which the distance between P(2, – 3) and Q(10, y) is 10 units are 3 and -9.
Question 9. If Q(0, 1) is equidistant from P(5,–3) and R(x,6), find the values of x. Also find the distances QR and PR.
Answer:
Given:
Point Q(0, 1) is equidistant from point P(5, -3) and point R(x, 6).
This means the distance QP is equal to the distance QR ($QP = QR$).
To Find:
The values of x.
The distance QR.
The distance PR.
Solution:
We use the distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Step 1: Find the value(s) of x.
Given that $QP = QR$, we can square both sides to work with $QP^2 = QR^2$. This avoids the square root.
Calculate the square of the distance QP (between Q(0, 1) and P(5, -3)):
$QP^2 = (5-0)^2 + (-3-1)^2$
$QP^2 = (5)^2 + (-4)^2$
$QP^2 = 25 + 16$
$QP^2 = 41$
Calculate the square of the distance QR (between Q(0, 1) and R(x, 6)):
$QR^2 = (x-0)^2 + (6-1)^2$
$QR^2 = x^2 + 5^2$
$QR^2 = x^2 + 25$
Set $QP^2$ equal to $QR^2$ as Q is equidistant from P and R:
$QP^2 = QR^2$
$41 = x^2 + 25$
Solve for $x^2$:
$x^2 = 41 - 25$
$x^2 = 16$
Take the square root of both sides to find the value(s) of x:
$x = \pm \sqrt{16}$
$x = \pm 4$
So, the possible values for x are 4 and -4.
Step 2: Find the distances QR and PR for each value of x.
We have two cases for the coordinates of point R: R(4, 6) when x = 4, and R(-4, 6) when x = -4.
Case 1: When x = 4, R is (4, 6).
Distance QR (between Q(0, 1) and R(4, 6)):
$QR = \sqrt{(4-0)^2 + (6-1)^2}$
$QR = \sqrt{4^2 + 5^2}$
$QR = \sqrt{16 + 25}$
$QR = \sqrt{41}$ units.
Distance PR (between P(5, -3) and R(4, 6)):
$PR = \sqrt{(4-5)^2 + (6-(-3))^2}$
$PR = \sqrt{(-1)^2 + (6+3)^2}$
$PR = \sqrt{(-1)^2 + 9^2}$
$PR = \sqrt{1 + 81}$
$PR = \sqrt{82}$ units.
Case 2: When x = -4, R is (-4, 6).
Distance QR (between Q(0, 1) and R(-4, 6)):
$QR = \sqrt{(-4-0)^2 + (6-1)^2}$
$QR = \sqrt{(-4)^2 + 5^2}$
$QR = \sqrt{16 + 25}$
$QR = \sqrt{41}$ units.
Distance PR (between P(5, -3) and R(-4, 6)):
$PR = \sqrt{(-4-5)^2 + (6-(-3))^2}$
$PR = \sqrt{(-9)^2 + (6+3)^2}$
$PR = \sqrt{(-9)^2 + 9^2}$
$PR = \sqrt{81 + 81}$
$PR = \sqrt{162}$
We can simplify $\sqrt{162}$ as $\sqrt{81 \times 2} = \sqrt{81} \times \sqrt{2} = 9\sqrt{2}$.
$PR = 9\sqrt{2}$ units.
Summary of Results:
The values of x are 4 and -4.
When x = 4:
QR = $\sqrt{41}$ units
PR = $\sqrt{82}$ units
When x = -4:
QR = $\sqrt{41}$ units
PR = $9\sqrt{2}$ units
Question 10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).
Answer:
Given:
A point P(x, y) which is equidistant from point A(3, 6) and point B(-3, 4).
To Find:
A relation between x and y.
Solution:
Let the point be P(x, y). The two given points are A(3, 6) and B(-3, 4).
According to the problem, the distance of P from A is equal to the distance of P from B.
$PA = PB$
We use the distance formula, which states that the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Using the distance formula for PA and PB:
$PA = \sqrt{(x-3)^2 + (y-6)^2}$
$PB = \sqrt{(-3-x)^2 + (4-y)^2}$
Since $PA = PB$, we have:
$\sqrt{(x-3)^2 + (y-6)^2} = \sqrt{(-3-x)^2 + (4-y)^2}$
Squaring both sides to eliminate the square root:
$(x-3)^2 + (y-6)^2 = (-3-x)^2 + (4-y)^2$
Note that $(-3-x)^2 = (-(3+x))^2 = (3+x)^2$.
So the equation becomes:
$(x-3)^2 + (y-6)^2 = (x+3)^2 + (4-y)^2$
Expand the squared terms using the identities $(a-b)^2 = a^2 - 2ab + b^2$ and $(a+b)^2 = a^2 + 2ab + b^2$:
$(x^2 - 6x + 9) + (y^2 - 12y + 36) = (x^2 + 6x + 9) + (16 - 8y + y^2)$
Combine the constant terms on each side:
$x^2 - 6x + y^2 - 12y + 45 = x^2 + 6x + y^2 - 8y + 25$
Subtract $x^2$ and $y^2$ from both sides of the equation:
$-6x - 12y + 45 = 6x - 8y + 25$
Move all terms to one side to form the relation. Let's move terms from the right side to the left side:
$-6x - 6x - 12y + 8y + 45 - 25 = 0$
Combine the like terms:
$(-6x - 6x) + (-12y + 8y) + (45 - 25) = 0$
$-12x - 4y + 20 = 0$
To simplify, divide the entire equation by -4:
$\frac{-12x}{-4} + \frac{-4y}{-4} + \frac{20}{-4} = \frac{0}{-4}$
$3x + y - 5 = 0$
This is the required relation between x and y.
The relation can also be expressed as $3x + y = 5$ or $y = -3x + 5$.
Example 6 to 10 (Before Exercise 7.2)
Example 6. Find the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally.
Answer:
Given:
Points A(4, -3) and B(8, 5).
A point P divides the line segment AB internally in the ratio $m_1 : m_2 = 3 : 1$.
To Find:
The coordinates of the point P(x, y).
Solution:
We use the Section Formula for internal division.
If a point P(x, y) divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, $(x_1, y_1) = (4, -3)$, $(x_2, y_2) = (8, 5)$, $m_1 = 3$, and $m_2 = 1$.
Calculate the x-coordinate of P:
$x = \frac{(3)(8) + (1)(4)}{3 + 1}$
$x = \frac{24 + 4}{4}$
$x = \frac{28}{4}$
$x = 7$
Calculate the y-coordinate of P:
$y = \frac{(3)(5) + (1)(-3)}{3 + 1}$
$y = \frac{15 - 3}{4}$
$y = \frac{12}{4}$
$y = 3$
So, the coordinates of the point P are (7, 3).
The point which divides the line segment joining (4, – 3) and (8, 5) in the ratio 3 : 1 internally is (7, 3).
Example 7. In what ratio does the point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8)?
Answer:
Given:
Points A(-6, 10) and B(3, -8).
A point P(-4, 6) divides the line segment AB.
To Find:
The ratio in which the point P(-4, 6) divides the line segment joining A(-6, 10) and B(3, -8).
Solution:
Let the point P(-4, 6) divide the line segment joining A(-6, 10) and B(3, -8) in the ratio $k : 1$.
We use the Section Formula for internal division. If a point P(x, y) divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, $(x_1, y_1) = (-6, 10)$, $(x_2, y_2) = (3, -8)$, P$(x, y) = (-4, 6)$, $m_1 = k$, and $m_2 = 1$.
Substitute the values into the formula for the x-coordinate:
$-4 = \frac{k(3) + 1(-6)}{k + 1}$
$-4 = \frac{3k - 6}{k + 1}$
Multiply both sides by $(k+1)$:
$-4(k + 1) = 3k - 6$
Expand the left side:
$-4k - 4 = 3k - 6$
Move the terms involving k to one side and constant terms to the other side:
$-4 - (-6) = 3k - (-4k)$
$-4 + 6 = 3k + 4k$
$2 = 7k$
Solve for k:
$k = \frac{2}{7}$
The ratio is $k : 1 = \frac{2}{7} : 1$.
To express the ratio as integers, multiply both parts by 7:
$(\frac{2}{7} \times 7) : (1 \times 7) = 2 : 7$
So, the ratio is 2 : 7.
We can verify this using the y-coordinate:
$6 = \frac{k(-8) + 1(10)}{k + 1}$
$6 = \frac{-8k + 10}{k + 1}$
$6(k + 1) = -8k + 10$
$6k + 6 = -8k + 10$
$6k + 8k = 10 - 6$
$14k = 4$
$k = \frac{4}{14} = \frac{2}{7}$
The ratio is $k : 1 = \frac{2}{7} : 1$, which is 2 : 7.
Since k is positive, the point P divides the line segment AB internally in the ratio 2 : 7.
The point (- 4, 6) divides the line segment joining A(– 6, 10) and B(3, – 8) in the ratio 2 : 7.
Example 8. Find the coordinates of the points of trisection (i.e., points dividing in three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4).
Answer:
Given:
The endpoints of the line segment are A(2, – 2) and B(– 7, 4).
To Find:
The coordinates of the points of trisection of the line segment AB.
Construction Required:
Draw a line segment AB. Mark two points P and Q on AB such that AP = PQ = QB. This means P is between A and Q, and Q is between P and B.
Solution:
Let the points of trisection of the line segment joining A(2, – 2) and B(– 7, 4) be P and Q.
These points divide the line segment into three equal parts, so AP = PQ = QB.
This implies that point P divides the line segment AB in the ratio $ AP : PB = AP : (PQ + QB) = 1 : (1 + 1) = 1 : 2 $.
Also, point Q divides the line segment AB in the ratio $ AQ : QB = (AP + PQ) : QB = (1 + 1) : 1 = 2 : 1 $.
We can find the coordinates of P and Q using the section formula. The section formula states that the coordinates of a point P$(x, y)$ that divides the line segment joining A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $ m_1 : m_2 $ are given by:
$ x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2} $
$ y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2} $
Here, $ (x_1, y_1) = (2, -2) $ and $ (x_2, y_2) = (-7, 4) $.
Step 1: Find the coordinates of point P.
Point P divides AB in the ratio $ m_1 : m_2 = 1 : 2 $.
Using the section formula for point P$(x_P, y_P)$:
$ x_P = \frac{(1)(-7) + (2)(2)}{1 + 2} = \frac{-7 + 4}{3} = \frac{-3}{3} = -1 $
$ y_P = \frac{(1)(4) + (2)(-2)}{1 + 2} = \frac{4 - 4}{3} = \frac{0}{3} = 0 $
So, the coordinates of the first point of trisection, P, are $ (-1, 0) $.
Step 2: Find the coordinates of point Q.
Point Q divides AB in the ratio $ m_1 : m_2 = 2 : 1 $.
Using the section formula for point Q$(x_Q, y_Q)$:
$ x_Q = \frac{(2)(-7) + (1)(2)}{2 + 1} = \frac{-14 + 2}{3} = \frac{-12}{3} = -4 $
$ y_Q = \frac{(2)(4) + (1)(-2)}{2 + 1} = \frac{8 - 2}{3} = \frac{6}{3} = 2 $
So, the coordinates of the second point of trisection, Q, are $ (-4, 2) $.
Alternate Method for Step 2 (Finding Q):
Since P and Q are points of trisection, P is the midpoint of AQ and Q is the midpoint of PB.
We can use the midpoint formula to find the coordinates of Q, considering Q as the midpoint of the segment PB, where P is $(-1, 0)$ and B is $(-7, 4)$.
The midpoint formula for a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is $ \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $.
If Q$(x_Q, y_Q)$ is the midpoint of PB, then P is $(-1, 0)$ and B is $(-7, 4)$.
$ x_Q = \frac{-1 + (-7)}{2} = \frac{-1 - 7}{2} = \frac{-8}{2} = -4 $
$ y_Q = \frac{0 + 4}{2} = \frac{4}{2} = 2 $
The coordinates of Q are $ (-4, 2) $, which matches the result obtained using the section formula directly for Q.
Answer:
The coordinates of the points of trisection of the line segment joining A(2, – 2) and B(– 7, 4) are (-1, 0) and (-4, 2).
Example 9. Find the ratio in which the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4). Also find the point of intersection.
Answer:
Given:
Two points A(5, -6) and B(-1, -4).
The y-axis divides the line segment joining A and B.
To Find:
The ratio in which the y-axis divides the line segment AB.
The coordinates of the point of intersection of the y-axis and the line segment AB.
Solution:
Let the point where the y-axis divides the line segment AB be P. Since the point P lies on the y-axis, its x-coordinate is 0. Let the coordinates of P be (0, y).
Let P(0, y) divide the line segment joining A(5, -6) and B(-1, -4) in the ratio $k : 1$.
We use the Section Formula for internal division. If a point P$(x, y)$ divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, $(x_1, y_1) = (5, -6)$, $(x_2, y_2) = (-1, -4)$, P$(x, y) = (0, y)$, $m_1 = k$, and $m_2 = 1$.
Step 1: Find the ratio k : 1.
Substitute the x-coordinates into the section formula for x:
$0 = \frac{k(-1) + 1(5)}{k + 1}$
$0 = \frac{-k + 5}{k + 1}$
For this fraction to be 0, the numerator must be 0 (assuming the denominator is not 0, which it is not if k is a finite number).
$-k + 5 = 0$
$-k = -5$
$k = 5$
So, the ratio $k : 1 = 5 : 1$.
Since the value of k is positive, the y-axis divides the line segment internally in the ratio 5 : 1.
Step 2: Find the coordinates of the point of intersection P(0, y).
Now use the value of the ratio ($k=5$, so $m_1=5, m_2=1$) and substitute the y-coordinates into the section formula for y:
$y = \frac{k y_2 + 1 y_1}{k + 1}$
$y = \frac{(5)(-4) + (1)(-6)}{5 + 1}$
$y = \frac{-20 - 6}{6}$
$y = \frac{-26}{6}$
Simplify the fraction:
$y = \frac{-13}{3}$
The coordinates of the point of intersection P are (0, y) = (0, $-\frac{13}{3}$).
The point of intersection is (0, $-\frac{13}{3}$).
Example 10. If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
Answer:
Given:
The points A(6, 1), B(8, 2), C(9, 4), and D(p, 3) are the vertices of a parallelogram, taken in order.
To Find:
The value of p.
Solution:
We know that the diagonals of a parallelogram bisect each other. This means that the midpoint of the diagonal AC is the same as the midpoint of the diagonal BD.
Let the vertices be A$(x_1, y_1) = (6, 1)$, B$(x_2, y_2) = (8, 2)$, C$(x_3, y_3) = (9, 4)$, and D$(x_4, y_4) = (p, 3)$.
The midpoint formula for a line segment joining points $(x_a, y_a)$ and $(x_b, y_b)$ is given by:
Midpoint = $(\frac{x_a+x_b}{2}, \frac{y_a+y_b}{2})$
Let's find the midpoint of the diagonal AC:
Midpoint of AC = $(\frac{6 + 9}{2}, \frac{1 + 4}{2})$
Midpoint of AC = $(\frac{15}{2}, \frac{5}{2})$
Now, let's find the midpoint of the diagonal BD:
Midpoint of BD = $(\frac{8 + p}{2}, \frac{2 + 3}{2})$
Midpoint of BD = $(\frac{8 + p}{2}, \frac{5}{2})$
Since the midpoints of AC and BD are the same:
$(\frac{15}{2}, \frac{5}{2}) = (\frac{8 + p}{2}, \frac{5}{2})$
Equating the x-coordinates of the midpoints:
$\frac{15}{2} = \frac{8 + p}{2}$
Multiply both sides by 2:
$15 = 8 + p$
Subtract 8 from both sides to solve for p:
$p = 15 - 8$
$p = 7$
Equating the y-coordinates would give $\frac{5}{2} = \frac{5}{2}$, which is consistent.
The value of p is 7.
Exercise 7.2
Question 1. Find the coordinates of the point which divides the join of (–1,7) and (4,–3) in the ratio 2 : 3.
Answer:
Given:
Points A$(-1, 7)$ and B$(4, -3)$.
A point P divides the line segment AB internally in the ratio $m_1 : m_2 = 2 : 3$.
To Find:
The coordinates of the point P(x, y) that divides the line segment.
Solution:
Let the given points be A$(x_1, y_1) = (-1, 7)$ and B$(x_2, y_2) = (4, -3)$.
Let the point P(x, y) divide the line segment AB in the ratio $m_1 : m_2 = 2 : 3$.
We use the Section Formula for internal division. The coordinates of the point P(x, y) are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Substitute the values into the formula for the x-coordinate:
$x = \frac{(2)(4) + (3)(-1)}{2 + 3}$
$x = \frac{8 - 3}{5}$
$x = \frac{5}{5}$
$x = 1$
Substitute the values into the formula for the y-coordinate:
$y = \frac{(2)(-3) + (3)(7)}{2 + 3}$
$y = \frac{-6 + 21}{5}$
$y = \frac{15}{5}$
$y = 3$
So, the coordinates of the point P are (1, 3).
The coordinates of the point which divides the join of (–1,7) and (4,–3) in the ratio 2 : 3 are (1, 3).
Question 2. Find the coordinates of the points of trisection of the line segment joining (4,–1) and (–2,–3).
Answer:
Given:
A line segment joining the points A(4, -1) and B(-2, -3).
To Find:
The coordinates of the points that divide the line segment AB into three equal parts (points of trisection).
Solution:
Let the given points be A(4, -1) and B(-2, -3).
Let the points of trisection be P and Q. These points divide the line segment AB into three equal parts, namely AP, PQ, and QB, such that $AP = PQ = QB$.
This means that point P divides the line segment AB in the ratio 1:2.
Point Q divides the line segment AB in the ratio 2:1.
We use the Section Formula for internal division. If a point P$(x, y)$ divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, the points are A$(x_1, y_1) = (4, -1)$ and B$(x_2, y_2) = (-2, -3)$.
Step 1: Find the coordinates of point P.
Point P divides AB in the ratio $m_1 : m_2 = 1 : 2$.
Coordinates of P$(x_P, y_P)$:
$x_P = \frac{(1)(-2) + (2)(4)}{1 + 2} = \frac{-2 + 8}{3} = \frac{6}{3} = 2$
$y_P = \frac{(1)(-3) + (2)(-1)}{1 + 2} = \frac{-3 - 2}{3} = \frac{-5}{3}$
So, the coordinates of point P are $(2, -\frac{5}{3})$.
Step 2: Find the coordinates of point Q.
Point Q divides AB in the ratio $m_1 : m_2 = 2 : 1$.
Coordinates of Q$(x_Q, y_Q)$:
$x_Q = \frac{(2)(-2) + (1)(4)}{2 + 1} = \frac{-4 + 4}{3} = \frac{0}{3} = 0$
$y_Q = \frac{(2)(-3) + (1)(-1)}{2 + 1} = \frac{-6 - 1}{3} = \frac{-7}{3}$
So, the coordinates of point Q are $(0, -\frac{7}{3})$.
The points of trisection of the line segment joining (4,–1) and (–2,–3) are (2, $-\frac{5}{3}$) and (0, $-\frac{7}{3}$).
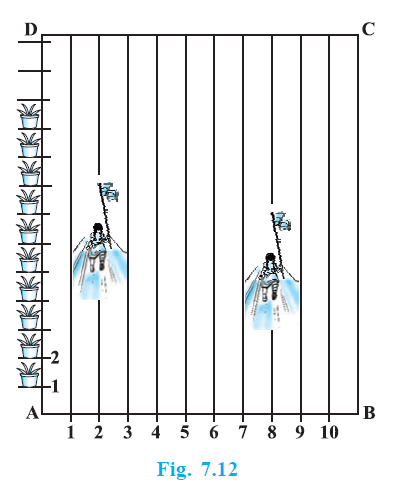
Question 3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs $\frac{1}{4}$ th the distance AD on the 2nd line and posts a green flag. Preet runs $\frac{1}{5}$ th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
Answer:
Given:
Lines are drawn 1m apart. 100 flower pots are placed 1m apart along AD.
Niharika posts a green flag running $\frac{1}{4}$th the distance AD on the 2nd line.
Preet posts a red flag running $\frac{1}{5}$th the distance AD on the eighth line.
Rashmi posts a blue flag exactly halfway between the two flags.
To Find:
The distance between the green and red flags.
The position (coordinates) where Rashmi should post her blue flag.
Solution:
Let's set up a coordinate system with A as the origin (0, 0). The lines drawn with chalk powder are parallel to AB, representing the x-coordinate. The lines are at distances 1m, 2m, 3m, ... from AD. So, the 2nd line corresponds to x = 2, and the 8th line corresponds to x = 8.
The flower pots are placed along AD at a distance of 1m from each other. AD is 100m long (since there are 100 pots 1m apart). Let AD lie along the y-axis. The distance run along AD corresponds to the y-coordinate.
Step 1: Determine the coordinates of Niharika's green flag.
Niharika runs on the 2nd line, so her x-coordinate is 2.
She runs $\frac{1}{4}$th the distance AD. Distance AD = 100m.
Distance run by Niharika $= \frac{1}{4} \times 100 = 25$m.
So, her y-coordinate is 25.
The coordinates of Niharika's green flag (G) are (2, 25).
Step 2: Determine the coordinates of Preet's red flag.
Preet runs on the eighth line, so his x-coordinate is 8.
He runs $\frac{1}{5}$th the distance AD. Distance AD = 100m.
Distance run by Preet $= \frac{1}{5} \times 100 = 20$m.
So, his y-coordinate is 20.
The coordinates of Preet's red flag (R) are (8, 20).
Step 3: Calculate the distance between the two flags.
We need to find the distance between G(2, 25) and R(8, 20) using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
$GR = \sqrt{(8-2)^2 + (20-25)^2}$
$GR = \sqrt{(6)^2 + (-5)^2}$
$GR = \sqrt{36 + 25}$
$GR = \sqrt{61}$
The distance between the two flags is $\sqrt{61}$ meters.
Step 4: Find the position of Rashmi's blue flag.
Rashmi posts her blue flag exactly halfway between the green flag (G) and the red flag (R).
This means Rashmi's flag is at the midpoint of the line segment GR.
We use the midpoint formula: Midpoint$(x, y) = (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$
The points are G(2, 25) and R(8, 20).
Let the coordinates of Rashmi's blue flag (B) be $(x_B, y_B)$.
$x_B = \frac{2 + 8}{2} = \frac{10}{2} = 5$
$y_B = \frac{25 + 20}{2} = \frac{45}{2} = 22.5$
The coordinates of Rashmi's blue flag are (5, 22.5).
Step 5: Interpret Rashmi's flag position in the context of the problem.
The x-coordinate is 5, which means Rashmi should post her flag on the 5th line.
The y-coordinate is 22.5, which means she should post her flag at a distance of 22.5 meters along AD from the starting point A. Since flower pots are 1m apart, this is between the 22nd and 23rd flower pot.
The distance between the two flags is $\sqrt{61}$ meters.
Rashmi should post her blue flag on the 5th line at a distance of 22.5 meters along AD.
Question 4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).
Answer:
Given:
Two points A(-3, 10) and B(6, -8).
A point P(-1, 6) divides the line segment AB.
To Find:
The ratio in which the point P(-1, 6) divides the line segment joining A(-3, 10) and B(6, -8).
Solution:
Let the point P(-1, 6) divide the line segment joining A(-3, 10) and B(6, -8) in the ratio $k : 1$.
We use the Section Formula for internal division. If a point P$(x, y)$ divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, $(x_1, y_1) = (-3, 10)$, $(x_2, y_2) = (6, -8)$, P$(x, y) = (-1, 6)$, $m_1 = k$, and $m_2 = 1$.
Substitute the values into the formula for the x-coordinate:
$-1 = \frac{k(6) + 1(-3)}{k + 1}$
$-1 = \frac{6k - 3}{k + 1}$
Multiply both sides by $(k+1)$:
$-1(k + 1) = 6k - 3$
$-k - 1 = 6k - 3$
Move the terms involving k to one side and constant terms to the other side:
$-1 + 3 = 6k + k$
$2 = 7k$
Solve for k:
$k = \frac{2}{7}$
The ratio is $k : 1 = \frac{2}{7} : 1$.
To express the ratio as integers, multiply both parts by 7:
$(\frac{2}{7} \times 7) : (1 \times 7) = 2 : 7$
Since the value of k is positive, the point P divides the line segment AB internally.
The ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6) is 2 : 7.
Question 5. Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer:
Given:
Two points A(1, -5) and B(-4, 5).
The line segment joining A and B is divided by the x-axis.
To Find:
The ratio in which the x-axis divides the line segment AB.
The coordinates of the point of division.
Solution:
Let the point where the x-axis divides the line segment AB be P. Since the point P lies on the x-axis, its y-coordinate is 0. Let the coordinates of P be (x, 0).
Let P(x, 0) divide the line segment joining A(1, -5) and B(-4, 5) in the ratio $k : 1$.
We use the Section Formula for internal division. If a point P$(x, y)$ divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, $(x_1, y_1) = (1, -5)$, $(x_2, y_2) = (-4, 5)$, P$(x, y) = (x, 0)$, $m_1 = k$, and $m_2 = 1$.
Step 1: Find the ratio k : 1.
Substitute the y-coordinates into the section formula for y:
$0 = \frac{k(5) + 1(-5)}{k + 1}$
$0 = \frac{5k - 5}{k + 1}$
For this fraction to be 0, the numerator must be 0 (assuming the denominator $k+1 \neq 0$).
$5k - 5 = 0$
$5k = 5$
$k = \frac{5}{5}$
$k = 1$
So, the ratio $k : 1 = 1 : 1$.
Since the value of k is positive (k=1), the x-axis divides the line segment internally in the ratio 1 : 1. This means the point of division is the midpoint.
Step 2: Find the coordinates of the point of division P(x, 0).
Now use the value of the ratio ($k=1$, so $m_1=1, m_2=1$) and substitute the x-coordinates into the section formula for x:
$x = \frac{k x_2 + 1 x_1}{k + 1}$
$x = \frac{(1)(-4) + (1)(1)}{1 + 1}$
$x = \frac{-4 + 1}{2}$
$x = \frac{-3}{2}$
The coordinates of the point of division P are (x, 0) = $(-\frac{3}{2}, 0)$.
The ratio in which the line segment is divided by the x-axis is 1 : 1, and the point of division is ($-\frac{3}{2}$, 0).
Question 6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer:
Given:
The points A(1, 2), B(4, y), C(x, 6), and D(3, 5) are the vertices of a parallelogram, taken in order.
To Find:
The values of x and y.
Solution:
We know that the diagonals of a parallelogram bisect each other. This means that the midpoint of the diagonal AC is the same as the midpoint of the diagonal BD.
Let the vertices be A$(x_1, y_1) = (1, 2)$, B$(x_2, y_2) = (4, y)$, C$(x_3, y_3) = (x, 6)$, and D$(x_4, y_4) = (3, 5)$.
The midpoint formula for a line segment joining points $(x_a, y_a)$ and $(x_b, y_b)$ is given by:
Midpoint = $(\frac{x_a+x_b}{2}, \frac{y_a+y_b}{2})$
Let's find the midpoint of the diagonal AC, joining A(1, 2) and C(x, 6):
Midpoint of AC = $(\frac{1 + x}{2}, \frac{2 + 6}{2})$
Midpoint of AC = $(\frac{1 + x}{2}, \frac{8}{2})$
Midpoint of AC = $(\frac{1 + x}{2}, 4)$
Now, let's find the midpoint of the diagonal BD, joining B(4, y) and D(3, 5):
Midpoint of BD = $(\frac{4 + 3}{2}, \frac{y + 5}{2})$
Midpoint of BD = $(\frac{7}{2}, \frac{y + 5}{2})$
Since the midpoints of AC and BD are the same, we equate their corresponding coordinates:
Equating the x-coordinates:
$\frac{1 + x}{2} = \frac{7}{2}$
Multiply both sides by 2:
$1 + x = 7$
$x = 7 - 1$
$x = 6$
Equating the y-coordinates:
$4 = \frac{y + 5}{2}$
Multiply both sides by 2:
$4 \times 2 = y + 5$
$8 = y + 5$
$y = 8 - 5$
$y = 3$
Thus, the values of x and y are 6 and 3 respectively.
The value of x is 6 and the value of y is 3.
Question 7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
Answer:
Given:
AB is the diameter of a circle.
The centre of the circle is C(2, – 3).
Point B is (1, 4).
To Find:
The coordinates of point A.
Solution:
Let the coordinates of point A be (x, y).
Let the coordinates of point B be $(x_2, y_2) = (1, 4)$.
Let the coordinates of the centre C be $(x_C, y_C) = (2, -3)$.
Since AB is the diameter and C is the centre of the circle, the centre C is the midpoint of the line segment AB.
We use the Midpoint Formula. The midpoint of a line segment with endpoints $(x_1, y_1)$ and $(x_2, y_2)$ is given by $(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$.
Using A(x, y) as $(x_1, y_1)$ and B(1, 4) as $(x_2, y_2)$, the midpoint (which is C(2, -3)) is:
$(x_C, y_C) = (\frac{x+1}{2}, \frac{y+4}{2})$
Substituting the coordinates of C:
$(2, -3) = (\frac{x+1}{2}, \frac{y+4}{2})$
Equating the corresponding coordinates:
Equating the x-coordinates:
$2 = \frac{x+1}{2}$
Multiply both sides by 2:
$2 \times 2 = x + 1$
$4 = x + 1$
Subtract 1 from both sides to solve for x:
$x = 4 - 1$
$x = 3$
Equating the y-coordinates:
$-3 = \frac{y+4}{2}$
Multiply both sides by 2:
$-3 \times 2 = y + 4$
$-6 = y + 4$
Subtract 4 from both sides to solve for y:
$y = -6 - 4$
$y = -10$
So, the coordinates of point A are (3, -10).
The coordinates of point A are (3, -10).
Question 8. If A and B are (– 2, – 2) and (2, – 4), respectively , find the coordinates of P such that AP = $\frac{3}{7}$ AB and P lies on the line segment AB.
Answer:
Given:
Points A(-2, -2) and B(2, -4).
Point P lies on the line segment AB such that $AP = \frac{3}{7} AB$.
To Find:
The coordinates of point P.
Solution:
Let the coordinates of point P be (x, y).
We are given that $AP = \frac{3}{7} AB$.
Since P lies on the line segment AB, we can write AB as the sum of AP and PB:
$AB = AP + PB$
Substitute the given relation $AP = \frac{3}{7} AB$ into this equation:
$AB = \frac{3}{7} AB + PB$
Subtract $\frac{3}{7} AB$ from both sides to find PB:
$PB = AB - \frac{3}{7} AB$
$PB = (1 - \frac{3}{7}) AB$
$PB = \frac{7-3}{7} AB$
$PB = \frac{4}{7} AB$
Now, we can find the ratio of AP to PB:
$\frac{AP}{PB} = \frac{\frac{3}{7} AB}{\frac{4}{7} AB}$
$\frac{AP}{PB} = \frac{3}{4}$
This means that point P divides the line segment AB internally in the ratio $AP : PB = 3 : 4$.
So, the ratio $m_1 : m_2 = 3 : 4$.
We use the Section Formula for internal division. If a point P(x, y) divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, A$(x_1, y_1) = (-2, -2)$, B$(x_2, y_2) = (2, -4)$, $m_1 = 3$, and $m_2 = 4$.
Calculate the x-coordinate of P:
$x = \frac{(3)(2) + (4)(-2)}{3 + 4}$
$x = \frac{6 - 8}{7}$
$x = \frac{-2}{7}$
Calculate the y-coordinate of P:
$y = \frac{(3)(-4) + (4)(-2)}{3 + 4}$
$y = \frac{-12 - 8}{7}$
$y = \frac{-20}{7}$
The coordinates of point P are $(-\frac{2}{7}, -\frac{20}{7})$.
Question 9. Find the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
Answer:
Given:
A line segment joining the points A(-2, 2) and B(2, 8).
To Find:
The coordinates of the points that divide the line segment AB into four equal parts.
Solution:
Let the given points be A(-2, 2) and B(2, 8).
Let the points that divide the line segment AB into four equal parts be P, Q, and R, such that AP = PQ = QR = RB.
This means:
1. Point P divides AB in the ratio 1:3 (AP is 1 part, PB = PQ + QR + RB = 3 parts).
2. Point Q divides AB in the ratio 2:2, which simplifies to 1:1. Thus, Q is the midpoint of AB.
3. Point R divides AB in the ratio 3:1 (AR = AP + PQ + QR = 3 parts, RB is 1 part).
We use the Section Formula for internal division. If a point P$(x, y)$ divides the line segment joining points A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m_1 : m_2$, then the coordinates of P are given by:
$x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}$
$y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}$
Here, A$(x_1, y_1) = (-2, 2)$ and B$(x_2, y_2) = (2, 8)$.
Step 1: Find the coordinates of point P.
Point P divides AB in the ratio $m_1 : m_2 = 1 : 3$.
Coordinates of P$(x_P, y_P)$:
$x_P = \frac{(1)(2) + (3)(-2)}{1 + 3} = \frac{2 - 6}{4} = \frac{-4}{4} = -1$
$y_P = \frac{(1)(8) + (3)(2)}{1 + 3} = \frac{8 + 6}{4} = \frac{14}{4} = \frac{7}{2}$
The coordinates of point P are $(-1, \frac{7}{2})$.
Step 2: Find the coordinates of point Q.
Point Q is the midpoint of AB. We can use the midpoint formula, which is a special case of the section formula with ratio 1:1.
Coordinates of Q$(x_Q, y_Q)$:
$x_Q = \frac{x_1 + x_2}{2} = \frac{-2 + 2}{2} = \frac{0}{2} = 0$
$y_Q = \frac{y_1 + y_2}{2} = \frac{2 + 8}{2} = \frac{10}{2} = 5$
The coordinates of point Q are $(0, 5)$.
Step 3: Find the coordinates of point R.
Point R divides AB in the ratio $m_1 : m_2 = 3 : 1$.
Coordinates of R$(x_R, y_R)$:
$x_R = \frac{(3)(2) + (1)(-2)}{3 + 1} = \frac{6 - 2}{4} = \frac{4}{4} = 1$
$y_R = \frac{(3)(8) + (1)(2)}{3 + 1} = \frac{24 + 2}{4} = \frac{26}{4} = \frac{13}{2}$
The coordinates of point R are $(1, \frac{13}{2})$.
The coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts are $(-1, \frac{7}{2})$, $(0, 5)$, and $(1, \frac{13}{2})$.
Question 10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in Order .
[Hint: Area of a rhombus = $\frac{1}{2}$ (product of its diagonals)]
Answer:
Given:
The vertices of a rhombus are A(3, 0), B(4, 5), C(-1, 4), and D(-2, -1) taken in order.
To Find:
The area of the rhombus ABCD.
Solution:
The vertices of the rhombus are A$(x_1, y_1) = (3, 0)$, B$(x_2, y_2) = (4, 5)$, C$(x_3, y_3) = (-1, 4)$, and D$(x_4, y_4) = (-2, -1)$.
The diagonals of the rhombus are AC and BD.
The area of a rhombus is given by the formula: Area $= \frac{1}{2} \times (\text{Length of diagonal 1}) \times (\text{Length of diagonal 2})$.
We will calculate the lengths of the diagonals AC and BD using the distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Step 1: Calculate the length of the diagonal AC.
Using points A(3, 0) and C(-1, 4):
$AC = \sqrt{(-1-3)^2 + (4-0)^2}$
$AC = \sqrt{(-4)^2 + (4)^2}$
$AC = \sqrt{16 + 16}$
$AC = \sqrt{32}$
$AC = \sqrt{16 \times 2} = 4\sqrt{2}$ units.
Step 2: Calculate the length of the diagonal BD.
Using points B(4, 5) and D(-2, -1):
$BD = \sqrt{(-2-4)^2 + (-1-5)^2}$
$BD = \sqrt{(-6)^2 + (-6)^2}$
$BD = \sqrt{36 + 36}$
$BD = \sqrt{72}$
$BD = \sqrt{36 \times 2} = 6\sqrt{2}$ units.
Step 3: Calculate the area of the rhombus.
Area $= \frac{1}{2} \times AC \times BD$
Area $= \frac{1}{2} \times (4\sqrt{2}) \times (6\sqrt{2})$
Area $= \frac{1}{2} \times (4 \times 6) \times (\sqrt{2} \times \sqrt{2})$
Area $= \frac{1}{2} \times 24 \times 2$
Area $= \frac{1}{2} \times 48$
Area $= 24$ square units.
The area of the rhombus is 24 square units.

